The Basis Patterns of DCT and iDCT Transform – Part 2
Contents
Last Post I have written The Basis Patterns of DCT and iDCT Transform – Part 1 as 1D array’s DCT transform. Now I try to produce the result of 2D matrix, which is usually used in Image & video processing.
When reading Iain E. Richardson’s book: The H.264 Advanced Video Compression Standard, 2nd edition, there are 4x4 DCT basis patterns & 8x8 DCT basis patterns on page 45. And beyond this book, these patterns come out almost at every book about Image Processing or Video Coding technology. Here is the question, how to get DCT basis pattern in above form of visual images.


DCT basis patterns on page 45 in the book
I have tried to use Python to get the DCT image which I called Big Show of DCT basis patterns.
First, we also get the mathematical formulas of how the DCT basis patterns are calculated. Here we don’t talk about how these formulas comes out. About the formulas, it is also a big topic which you should check a topic book.
Consider the MxN - point image as a MxN - dimensional array (matrix)
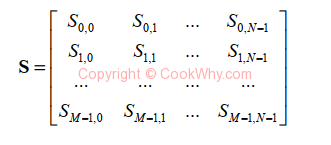
The inverse transform says that S can be represented as the sum of MxN basis images
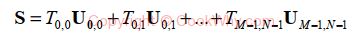
where Ukl corresponds to the (k , l ) - th transform kernel :
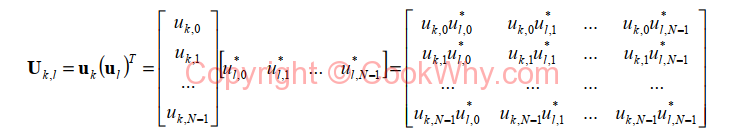
The forward transform says that the expansion coefficient Sk can be determined by the inner product of S and Ukl:
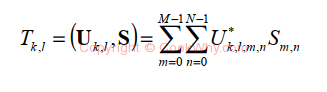
Where U is basis vector
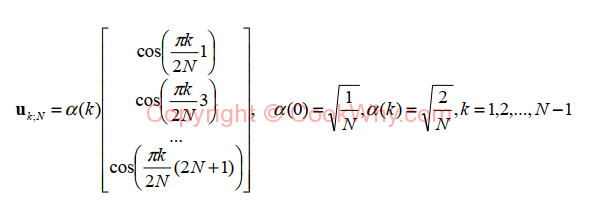
and all these U forms a matrix of MxN matrix, which every element is also a MxN matrix.
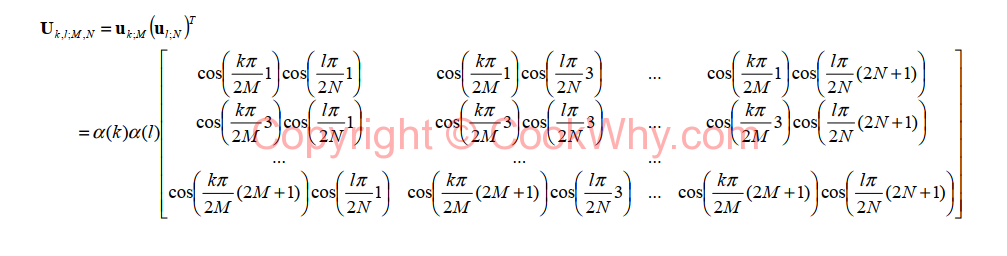
The key point is to generate right U basis pattern. First, we get A by following code:
[code lang=“python”] # init basis prefix A = np.zeros(N) A[0] = np.sqrt(1/N) for k in range(1, N): A[k] = np.sqrt(2/N) [/code]
Second, we generate basis patter of 1D:
[code lang=“python”] #generate basis patterns U_1D = np.zeros((N, N)) for k in range(0, N): for n in range(0, N): U_1D[k][n] = np.cos( (k*(2*n+1)/(2*N))*np.pi ) U_1D[k] = np.round(U_1D[k] * A[k], 4) [/code]
Third, use the reverse vector to get full of MxN basis pattern:
[code lang=“python”] U = np.zeros((N, N, N, N)) for k in range(0, N): for j in range(0, N): #calculate the k,j of N,N block temp = U_1D[k].reshape(N, 1) U[k][j] = np.multiply(temp, U_1D[j]) print(" Row %d, column %d" % (k, j)) print(U[k][j]) [/code]
Here please pay attention to np.multiply function. By using this, we should use np.reshape instead of np.transpose for np.array to reshape to vector.
By now, we have gotten the DCT basis pattern which is named U in my code. Then we convert the basis pattern to a big image.
[code lang=“python”] margin = 1 # margin pixel of the bigshow # key steps for normalization, must use mean as initialization mean = (np.max(U) - np.min(U))/2 bigShow = np.full((N*N+margin*(N-1), N*N+margin*(N-1)), mean)
for k in range(0, N): for j in range(0, N): row = k*N + k*margin column = j*N + j*margin for m in range(0, N): for n in range(0, N): bigShow[row+m][column+n] = U[k][j][m][n]
bigShow = normalization(bigShow) plt.figure() plt.imshow(bigShow, cmap=‘gray’) plt.title( “%dx%d basis pattern block” % (N, N)) plt.show() [/code]
For 4x4 test data, I get following basis pattern.
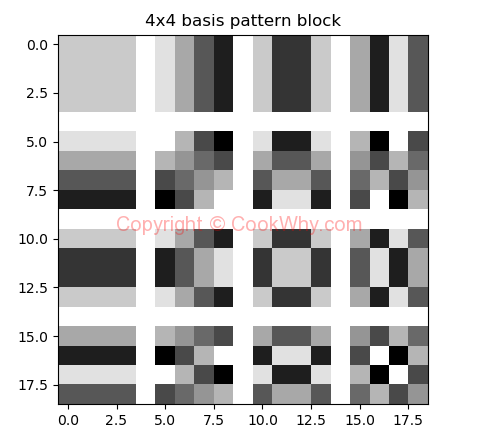
Big Show of 4x4 DCT basis patterns
And for 8x8 test data, I get following basis pattern.
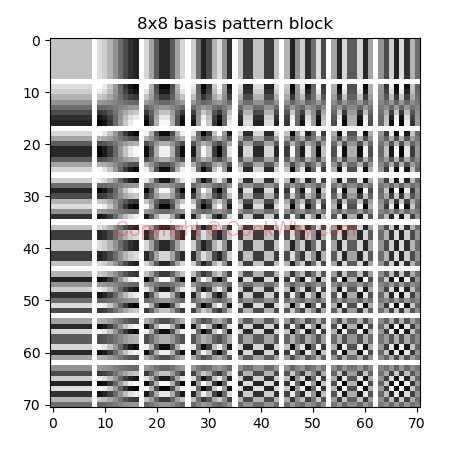
Big Show of 8x8 DCT basis patterns
The 2D DCT basis pattern image is so beautiful, is it right?
Now we can use one 4x4 & 8x8 test data to do DCT forward and inverse transform to verify the code. Use following code to get the coefficients of input 2D matrix.
[code lang=“python”] for k in range(0, N): for j in range(0, N): T[k][j] = np.multiply(U[k][j], S).sum() [/code]
The 4x4 matrix is:

The coefficients after calculation is
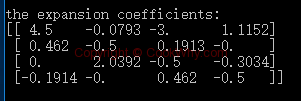
If we use inverse transform to get the data back, we will see the data is almost the same as origin ones.
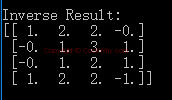
The 8x8 matrix is:
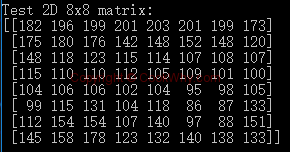
The coefficients after calculation is
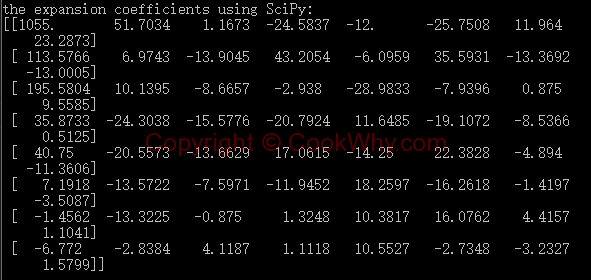
If we use inverse transform to get the data back, we will see the data is almost the same as origin ones.
In my code, I also provide a way using Python’s own function to calculate DCT and iDCT. If you are interesting about this, you will find that the result is the same as mine.
Some Tips:
1. Use a 4D matrix which is generated by following code to construct the basis patterns.
[code lang=“python”] U_mn = np.zeros((N, N, N, N)) [/code]
2. For one colunm vector, should use
[code lang=“python”] np.multiply [/code]
to replace np.dot, or else the result will be the inner production of vectors.
Full Reference code:
[code lang=“python”] # use dct formula to do dct & idct calculation import numpy as np from scipy.fftpack import fft, dct import scipy import matplotlib.pyplot as plt import matplotlib
def img2dct(a): return scipy.fftpack.dct( scipy.fftpack.dct( a, axis=0, norm=‘ortho’ ), axis=1, norm=‘ortho’ )
def dct2img(a): return scipy.fftpack.idct( scipy.fftpack.idct( a, axis=0 , norm=‘ortho’), axis=1 , norm=‘ortho’)
def normalization(data): _range = np.max(data) - np.min(data) return (data - np.min(data)) / _range
#show all the block in big image, with two margin within two block # U is 4D array, which is N*N matrix’s basis pattern def showBasisPatternTogether(U, N=4): margin = 1 # margin pixel of the bigshow # key steps for normalization, must use mean as initialization mean = (np.max(U) - np.min(U))/2 bigShow = np.full((N*N+margin*(N-1), N*N+margin*(N-1)), mean)
for k in range(0, N): for j in range(0, N): row = k*N + k*margin column = j*N + j*margin for m in range(0, N): for n in range(0, N): bigShow[row+m][column+n] = U[k][j][m][n]
bigShow = normalization(bigShow) plt.figure() plt.imshow(bigShow, cmap=‘gray’) plt.title( “%dx%d basis pattern block” % (N, N)) plt.show()
def dct_detail(S, N = 4): # init basis prefix A = np.zeros(N) A[0] = np.sqrt(1/N) for k in range(1, N): A[k] = np.sqrt(2/N) #generate basis patterns U_1D = np.zeros((N, N)) for k in range(0, N): for n in range(0, N): U_1D[k][n] = np.cos( (k*(2*n+1)/(2*N))*np.pi ) U_1D[k] = np.round(U_1D[k] * A[k], 4)
#use the reverse vector to get the kj of N*N block U = np.zeros((N, N, N, N)) for k in range(0, N): for j in range(0, N): #calculate the k,j of N,N block temp = U_1D[k].reshape(N, 1) U[k][j] = np.multiply(temp, U_1D[j])
# show basis pattern showBasisPatternTogether(U, N)
# plt.figure() # print(U[0][0]) # plt.imshow(U[0][0], cmap=‘gray’, vmin=0, vmax=1) # plt.title( “An 4x4 coefficients block”) # plt.show()
T = np.zeros((N, N)) # forward transform, calculate the expansion coefficients for k in range(0, N): for j in range(0, N): T[k][j] = np.multiply(U[k][j], S).sum()
print("\nthe expansion coefficients:") T = np.around(T, 4) print(T)
# inverse transform, calculate the S by coefficients & basis S_inverse = np.zeros([N, N]) for k in range(0, N): for j in range(0, N): S_inverse = S_inverse + T[k][j]*U[k][j] print("\nInverse Result:") print(np.round(S_inverse,0))
if __name__ == “__main__”: np.set_printoptions(suppress=True)
# 4x4 block test data set N = 4 S = np.array([[1, 2, 2, 0], [0, 1, 3, 1], [0, 1, 2, 1], [1, 2, 2, -1]])
# real 8x8 image test data # N = 8 # S = np.array([[182, 196, 199, 201, 203, 201, 199, 173], # [175, 180, 176, 142, 148, 152, 148, 120], # [148, 118, 123, 115, 114, 107, 108, 107], # [115, 110, 110, 112, 105, 109, 101, 100], # [104, 106, 106, 102, 104, 95, 98, 105], # [99, 115, 131, 104, 118, 86, 87, 133], # [112, 154, 154, 107, 140, 97, 88, 151], # [145, 158, 178, 123, 132, 140, 138, 133]])
# random test data # N = 8 # axis of 1D vector # S = np.random.randint(0, 100, size=[N, N]) print("\nTest 2D %dx%d matrix:" % (N, N)) print(S)
# calculate DCT patterns by formula dct_detail(S, N)
# check the coefficients by Scipy T_scipy = np.round(img2dct(S), 4) print("\nthe expansion coefficients using SciPy:") print(T_scipy)
#something wrong with below calculation S_scipy = np.round(dct2img(T_scipy), 4) print("\nInverse Result using SciPy:") print(S_scipy) [/code]
Reference:
Author Watterry
LastMod 2019-12-24
