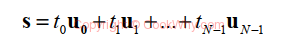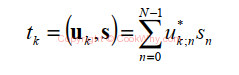The Basis Patterns of DCT and iDCT Transform - Part 1
Contents
Last post I have written about DCT and iDCT transform of a 2D image which is also a 2D matrix. There is a A matrix which is used to calculate DCT transform Y of original matrix X. The A is provided by the book directly, but how A is calculated out? Today I will talk about the original of matrix A. This is the first part of the topic which will focus on 1D vector transform.
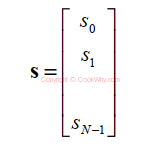
Consider the point signal s(n) as an N - dimensional vector, for example:
The inverse transform says that S can be represented as the sum of N basis vectors
where Uk corresponds to the k - th transform kernel:
The forward transform says that the expansion coefficient t can be determined by the inner product S of with U:
The U is the basis vectors named patterns of DCT transform, which can be considered “real” version of DFT. The U is calculated by following formula and the theory behind the formula is very complex which is out of the topic today.
I write some Python code to provide the process of DCT itself.
First, we provide the basis prefix of A:
[code lang=“python”] # init basis prefix A = np.zeros(N) A[0] = np.sqrt(1/N) for k in range(1, N): A[k] = np.sqrt(2/N)
[/code]
Second, we provide U itself:
[code lang=“python”] #generate basis patterns U = np.zeros((N, N)) for k in range(0, N): for n in range(0, N): U[k][n] = np.cos( (k*(2*n+1)/(2*N))*np.pi ) U[k] = np.round(U[k] * A[k], 4) [/code]
By the time, we have get the expansion coefficients of original numbers.
Finally, we try to do the inverse transform and check the result whether it is the same as the original number vectors.
[code lang=“python”] # inverse transform, calculate the S by coefficients & basis S_inverse = np.zeros(N) for k in range(0, N): S_inverse = S_inverse + T[k]*U[k] print("\nInverse Result:") print(np.round(S_inverse,0)) [/code]
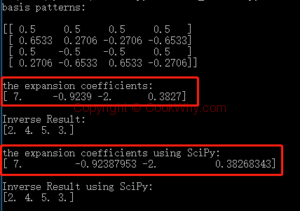
I also use SciPy to check my result, the result is the same as my handwrite code. I use (2, 4, 5, 3) vector as example, here show the result:
In all applications, the U basis pattern will never change, so basis T will be another expression way of vector number. That’s the meaning of another domain of data!
Here is my complete sample code.
[code lang=“python”] # use dct formula to do dct & idct calculation import numpy as np from scipy.fftpack import fft, dct import scipy
def dct_detail(S, N = 4): # init basis prefix A = np.zeros(N) A[0] = np.sqrt(1/N) for k in range(1, N): A[k] = np.sqrt(2/N) #generate basis patterns U = np.zeros((N, N)) for k in range(0, N): for n in range(0, N): U[k][n] = np.cos( (k*(2*n+1)/(2*N))*np.pi ) U[k] = np.round(U[k] * A[k], 4)
print(“basis patterns:\n”) print(U)
T = np.zeros(N) # forward transform, calculate the expansion coefficients for k in range(0, N): # the 1st way to calculate the inner product #t[k] = np.inner(U[k], S) # the 2nd way to calculate the inner product T[k] = sum(U[k][:]*S[:])
print("\nthe expansion coefficients:") print(T)
# inverse transform, calculate the S by coefficients & basis S_inverse = np.zeros(N) for k in range(0, N): S_inverse = S_inverse + T[k]*U[k] print("\nInverse Result:") print(np.round(S_inverse,0))
if __name__ == “__main__”: # test data set N = 4 S = np.array([2, 4, 5, 3])
# random test data # N = 8 # axis of 1D vector # S = np.random.randint(0, 100, size=[N]) # print("\nTest 1D number vector:") # print(S)
# calculate DCT patterns by formula dct_detail(S, N)
# check the coefficients by Scipy T_scipy = scipy.fftpack.dct( S, axis=0, norm=‘ortho’ ) print("\nthe expansion coefficients using SciPy:") print(T_scipy) S_scipy = scipy.fftpack.idct( T_scipy, axis=0 , norm=‘ortho’) print("\nInverse Result using SciPy:") print(S_scipy) [/code]
Reference: